The academic definition of ‘lift’ refers to the work done by a solar water pump on a unit weight of liquid, i.e., the increase in energy of a unit weight of liquid after it passes through the solar water pump.

However, in practical applications, lift is not expressed in units of energy, but rather as liquid column height (H), measured in meters (m). Other common units for lift include kilograms (kg) and megapascals (mpa), with the conversion relationship being: 1mpa = 10kg = 100m.

Solar water pump lift is a crucial working parameter for the solar water pump and plays a key role in the selection of solar water pumps. It determines whether the solar water pump can deliver water to the required location.

If the lift is too low, the water won’t reach its destination. Conversely, if the lift is too high, it can lead to increased power usage and electricity costs, and potentially cause the motor to overheat and fail.

For industry professionals, calculating solar water pump head is an essential skill. Hober will now detail the method for calculating solar water pump head.

Solar Water Pump Head Calculation

According to standard formulas, solar water pump head (H) is calculated as: H = z + hw

• ‘z’ represents the vertical rise of the water, or the height difference from the water surface at the entry point to that at the exit point.
• ‘hw’ is the head loss, which includes both the head loss along the path (hf) and local head loss (hw).

Head loss (hf) is calculated using Darcy’s formula or Xie Cai’s formula:

hw = ξ * v² / 2g

• ξ is the local head loss coefficient. For its value, please refer to relevant literature.
• v is the flow velocity in the pipe. Generally, hw occurs at points like the entrance, bends, valves, and outlets.

However, this calculation is often not performed in practical applications. Let’s focus on how to calculate solar pump head in actual project budgets.

Practical Solar Water Pump Head Calculation

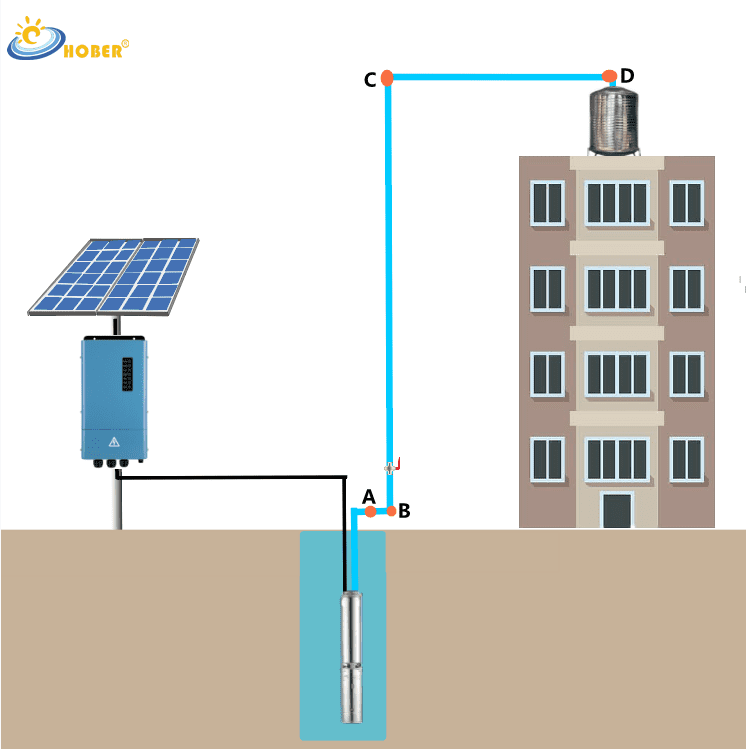
Consider this scenario: transporting water from a pool to the third floor rooftop. With ‘A’ representing the solar water pump and ‘123’ indicating the floors, under ideal conditions, the solar water pump lift can be simply understood as the vertical distance from point B to C. This height, usually in meters, represents the pump head.

Note that the height from B to C refers to vertical height, not pipeline length. If the route from B to C is sloped, the vertical height must be calculated.

In real-world operations, the pumped liquid doesn’t move straight up or down but travels horizontally and through bends and tees. These represent losses, so they must be considered in calculating pump lift.

If the liquid is clean water at normal temperature and the pipeline is made of PVC or steel, the following rough estimates can be used:

• 1 elbow ≈ 0.5 meter of solar water pump head loss
• 10 meters of horizontal distance ≈ 1 meter of pump head loss

Using the above example, if the horizontal distance from A to B is 10 meters, the vertical height from B to C is 20 meters, and the horizontal distance from C to D is 10 meters, then the required pump head is:

1 + 0.5 + 20 + 0.5 + 1 = 23 meters [10 meters horizontal distance AB + elbow loss at point B + vertical distance BC + elbow loss at point C + 10 meters horizontal distance CD]

With this quick calculation method, you’ve essentially completed a basic course in solar water pump head calculation. However, in real applications, pipelines are often not strictly horizontal or vertical, and may include inclined sections.

Don’t worry, Hober will introduce the ultimate solar water pump lift calculation method below.

The calculation method for solar water pump head is:

Pump head = vertical height + pipeline loss + outlet pressure

Let’s break these down:

1. Vertical Height
   • This refers to the vertical height difference between the center point of the solar water pump outlet and the pipeline’s end point.
   • If the height difference is substantial (over 100 meters), it’s considered as the height difference from the horizontal plane to the end of the pipeline, effectively ignoring the suction lift of three to five meters.
2. Pipeline Loss
   • Pipeline loss refers to the energy loss when liquid flows through the pipeline, including friction loss and accessory loss (like valves and elbows).
   • Calculating pipeline loss is complex and requires knowing the flow rate (Q in m³/h), pipe diameter (DN in mm), total pipeline length (in meters), pipeline material, and the number of accessories such as valves, tees, or elbows.
3. Outlet Pressure
   • This is the water pressure at the end of the pipe.
   • Often, the goal isn’t just to lift water but to also ensure a specific pressure at the outlet. For instance, if pumping river water up a mountain for sprinkler irrigation, the water needs enough pressure at the mountaintop to facilitate spraying.

Practical Example

Let’s apply this to a real-world scenario:

Suppose a project requires a flow rate of 200m³/h, a total pipeline length of 1100 meters, an unknown vertical height, a slope of 30 degrees, a plan to use DN200mm seamless steel pipe, and a required outlet pressure of 10kg. What would the pump lift be?

• Calculate the vertical height: At 30 degrees, the sine function value is approximately 0.523. Hence, 1100 meters * 0.523 = 575 meters, indicating a vertical height of 575 meters.
• Pipeline loss: For DN200mm and Q=200m³/h, the loss per 100 meters is 2.1 meters. For 1100 meters, this amounts to 23.1 meters.
• Required outlet pressure: 10kg, equivalent to roughly 100 meters.

Thus, the total design head for this solar water pump is: 575 + 23.1 + 100 = 698.1 meters. Including the losses from valves and elbows, the pump head should be no less than 700 meters.

Key Considerations When Selecting a Solar Water Pump

It’s crucial to determine the appropriate lift for a solar water pump. Incorrect lift selection can lead to inefficiencies, excessive power consumption, and even mechanical failures or motor burnout. For instance, a stainless steel submersible solar pump with a lift of 15 meters might be selected for an industrial application, but if only 10 meters is needed, this can cause operational issues such as excessive vibration. Adjusting the valve at the pump outlet can mitigate this, but it also leads to wasted electricity and increased costs.

Therefore, calculate the lift close to the actual requirement and avoid large margins. For instance, if the solar water pump height is 20 meters and the horizontal pipe is a DN50 pipe extending 100 meters, consider the loss from the horizontal pipe and additional factors such as elbows and valves. For water transportation, a solar pump lift of 27-30 meters could be suitable. For specific loss calculations, consulting Hober engineers is advised.

When calculating head, avoid misconceptions. The head is not just the vertical height or pipeline length. It’s essential to consider flow rate, total pipeline length, diameter, and material, balancing initial investment against operating costs. Remember the unit conversion method and confirm details with the manufacturer’s technical personnel if needed.